Nonlinear approximation of images

Prerequisites: You will need to download Wavelab850.

First load an image:

% image=double(imread('images/boat512.tif'))/255;
image = phantom(512);
image = image(1:256,1:256);
N = 2^floor(log2(length(image)));
image = image(1:N,1:N)/max(image(:));

Plot the wavelet coefficients of this image:

a=2; %number of vanishing moments

%% periodic wavelet
filter = MakeONFilter('Daubechies',2*a);
L = 4;
wc    = FWT2_PO(image,L,filter);
% wc    = FWT2_CDJV(image,L,a); uncomment for boundary wavelets

figure;
imagesc(wc, [0 1]); colormap('gray');

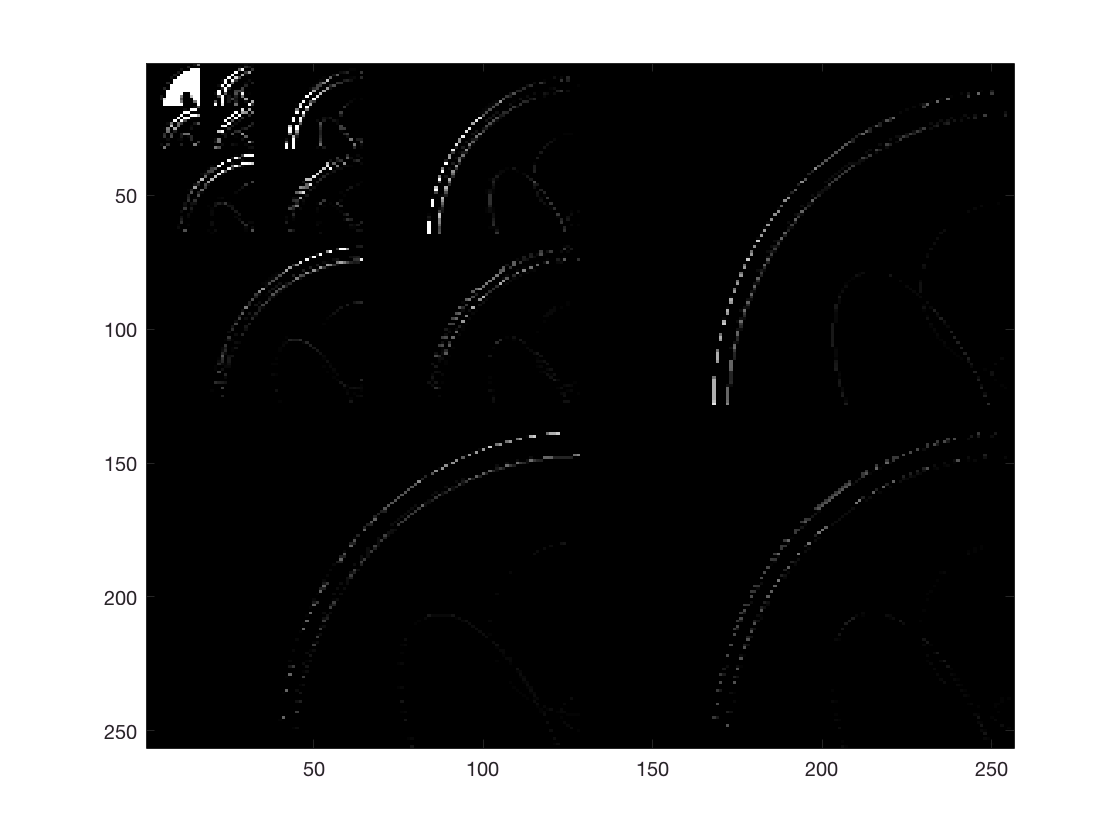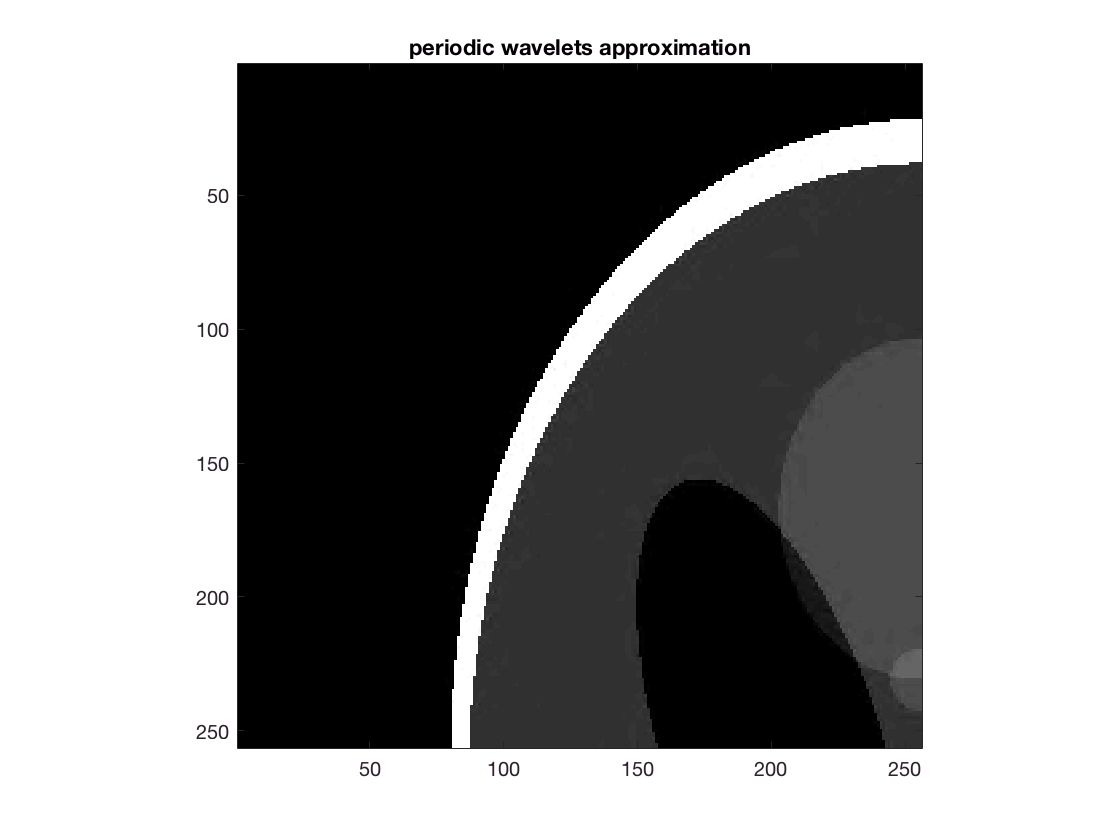
Compute its nonlinear wavelet approximation from the largest 5% of its coefficients:

[~,indx] = sort(abs(wc(:)), 'descend');
ratio =0.05;
p = ceil(sqrt(ratio*N^2/4));
ratiowc = zeros(N);
ratiowc(indx(1:4*p^2)) = wc(indx(1:4*p^2));
daubf = IWT2_PO(ratiowc,L,filter);
% daubf = IWT2_CDJV(ratiowc,L,a); %uncomment for boundary wavelets
error_wav = norm(image-daubf)/norm(image)
% error_wav = 0.0048

figure;
imagesc(daubf, [0 1]); colormap('gray')
title('periodic wavelets approximation')
axis square

Compute the Fourier nonlinear approximation:

%% fourier
hat = fft2(image);
[~,indx] = sort(abs(hat(:)), 'descend');
fc = zeros(N);
fc(indx(1:4*p^2)) = hat(indx(1:4*p^2));
fourf = ifft2(fc);
err_four = norm(image-fourf)/norm(image)
% err_four = 0.0633

figure;
imagesc(real(fourf));  title('Fourier');
colormap('gray')
axis square